[最も欲しかった] 30 60 90 üçgeni Kenarları 243336-30 60 90 üçgeni Kenarları
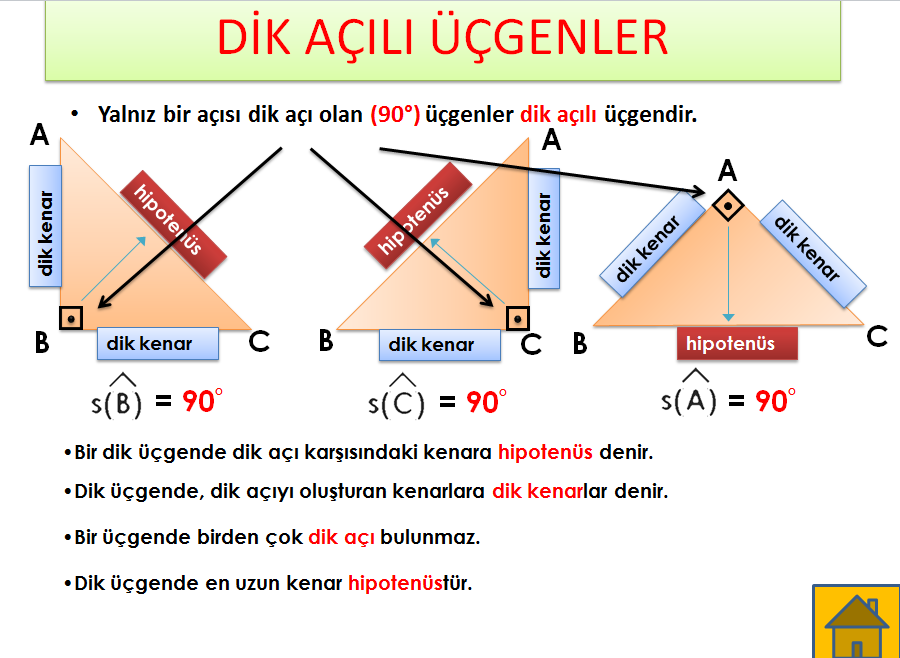
Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir
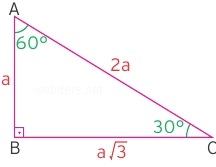
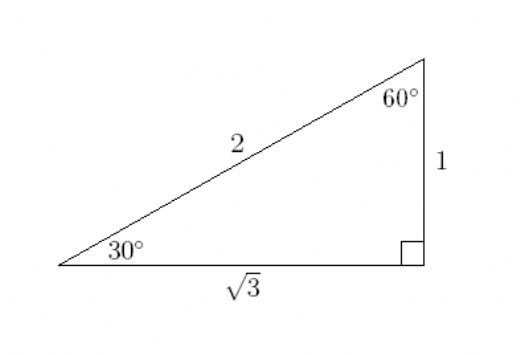
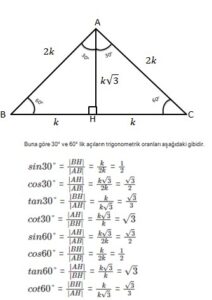
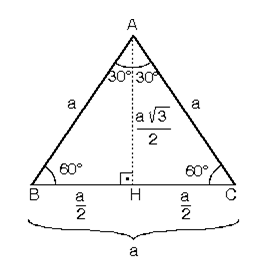
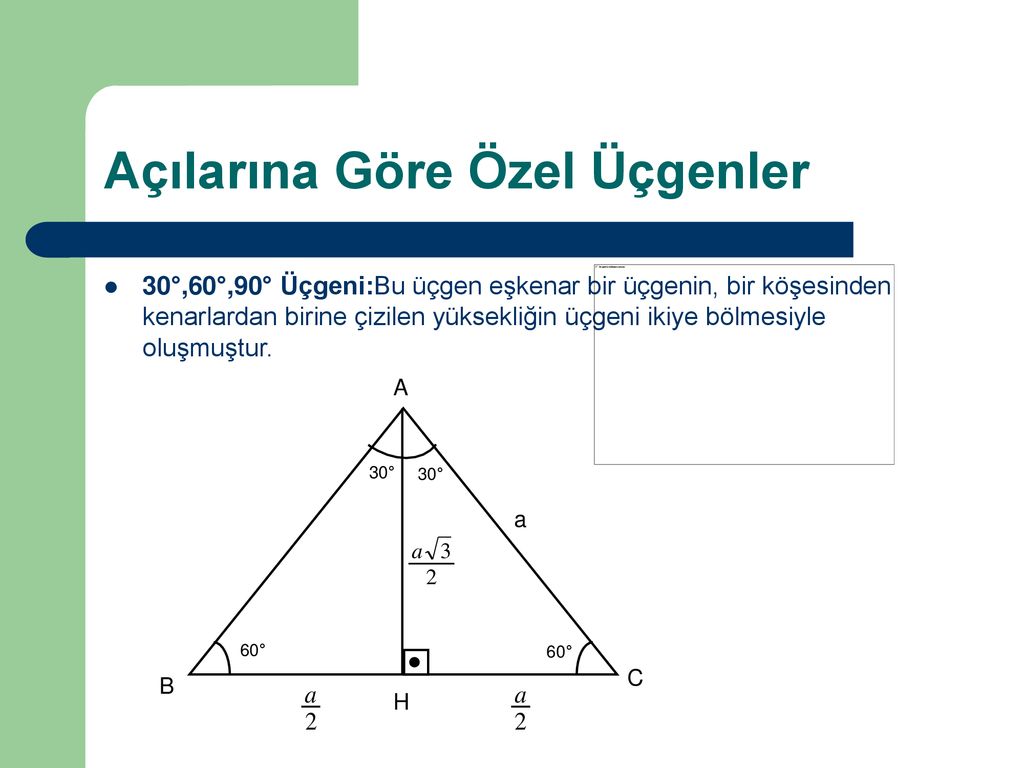
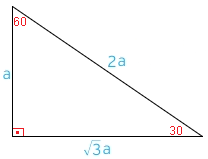
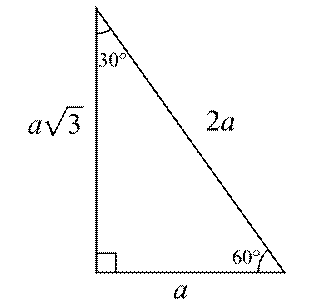
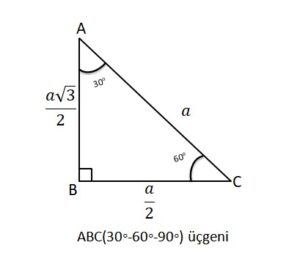
4 (30° – 60° – 90°) Üçgeni ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABH ve ACH (30° 60° 90°) üçgenleri elde edilir AB = AC = a BH = HC = pisagordan (30° 60° 90°) dik üçgeninde;30 – 60 – 90 ÜÇGENİ Eşkenar üçgende bir kenara ait yükseklik çizilirse oluşan iki dik üçgenin de açıları 30° – 60° – 90° olur Bu eşkenar üçgenin bir kenarının uzunluğunu 2a kabul edersek, oluşan dik üçgenlerde 30 derecelik açının karşısı a olur çünkü yükseklik aynı zamanda kenarortaydır
30 60 90 üçgeni kenarları
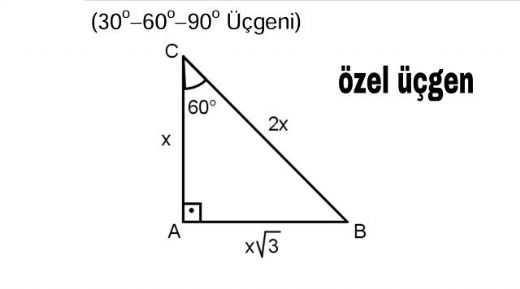
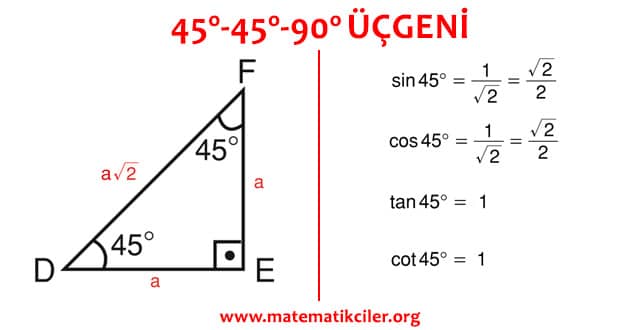
30 60 90 üçgeni kenarları-30°'nin karşısındaki kenar hipotenüsün yarısına eşittir 60° nin karşısındaki kenar, 30° nin45 45 90 üçgeni çözmek, çözülmesi en basit sağ kenarlı üçgendir Pisagor teoremini aşağıdaki gibi uygulamanız yeterlidir a = birinci kenar uzunluğu b = ikinci kenar uzunluğu (birinci kenara eşittir) c = hipotenüs Pisagor formülü a² b² = c² c = √ (2a²) = a√2 A = Alan
30 60 90 Ucgeni Ozellikleri Nelerdir
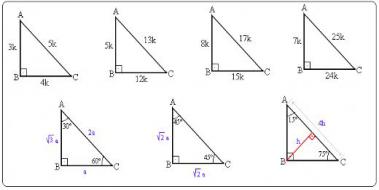
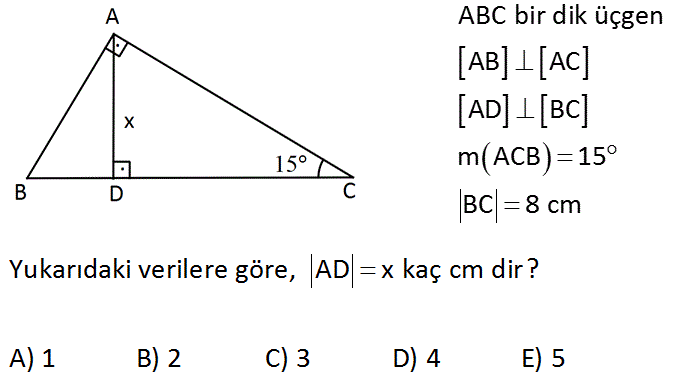
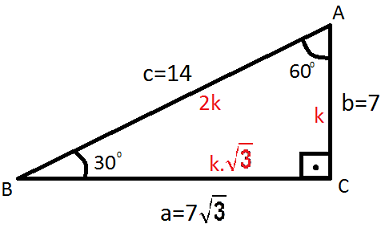
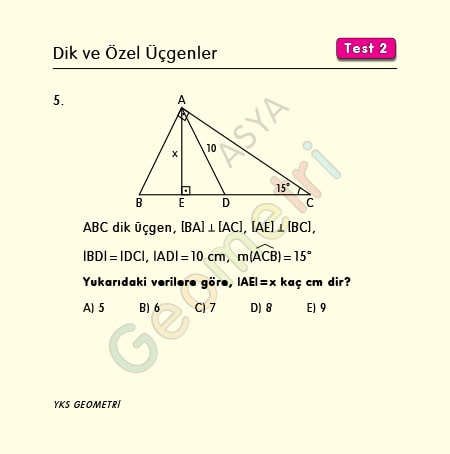
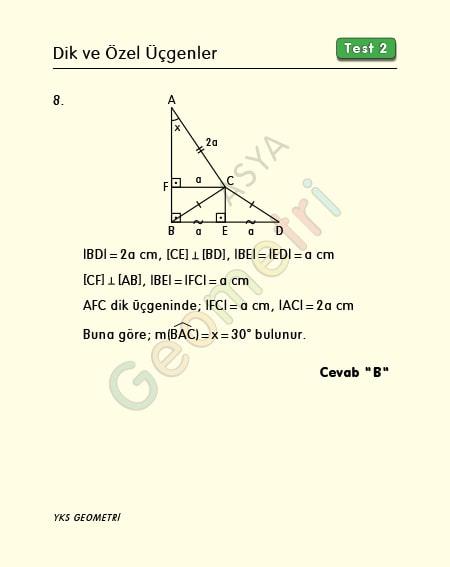
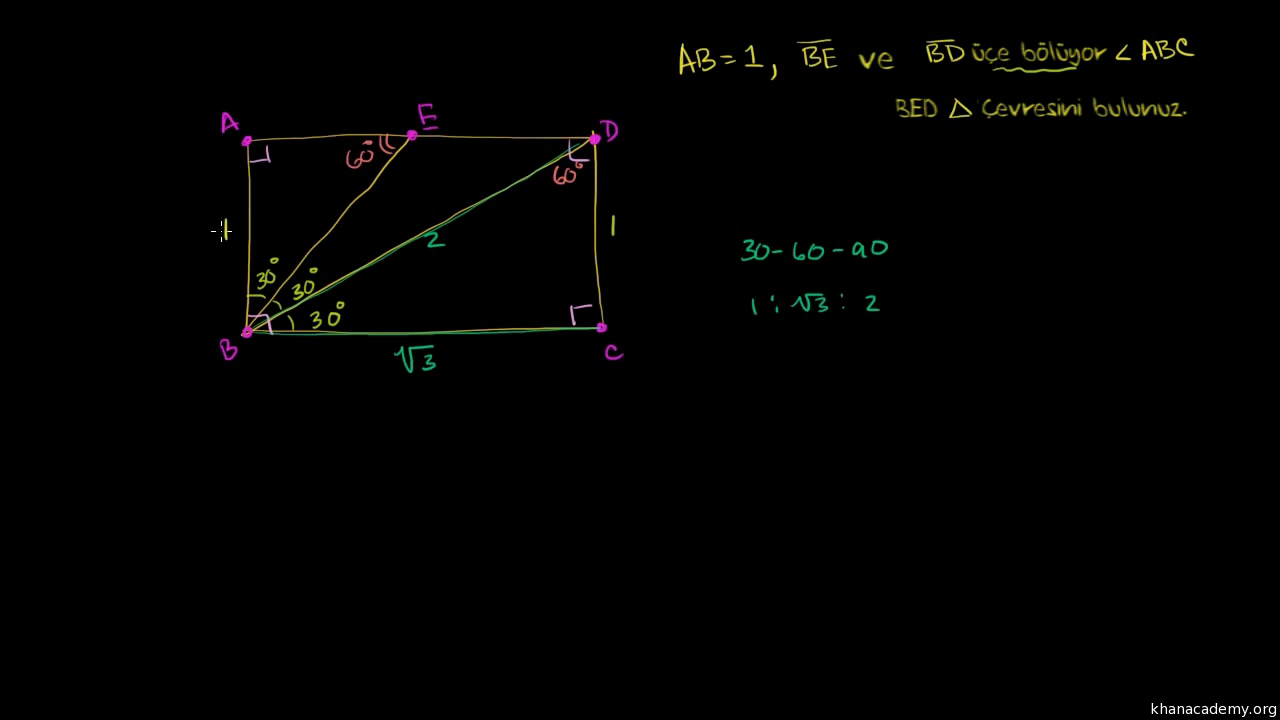
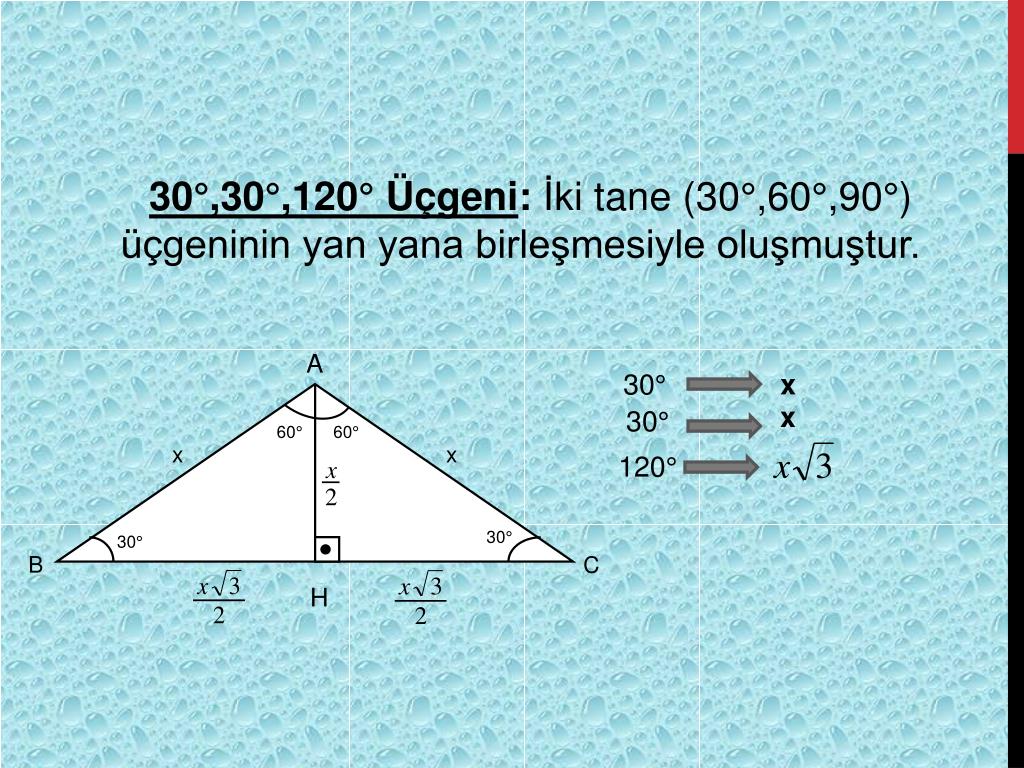
8 AB 4 cm dir 2 60 nin karşısı, 30 nin karşısının 3 katıdır x 4 3 cm buluruz 5530°'nin karşısındaki kenar hipotenüsün yarısına eşittir 60° nin karşısındaki kenar, 30° nin karşısındaki kenarın Ö3 katıdır 5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1°Özel dik üçgen Special right triangle " üçgen" buraya yönlendirir Çizim aracı için bkz kare karesi " üçgen" buraya yönlendirir Çizim aracı için kare kareye bakın Bazı özel üçgenlerin , ikizkenar üçgenlerin en az iki eşit kenara sahip olduğu, yani eşkenar üçgenlerin
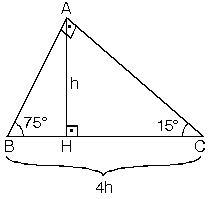
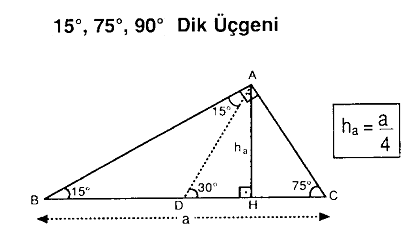
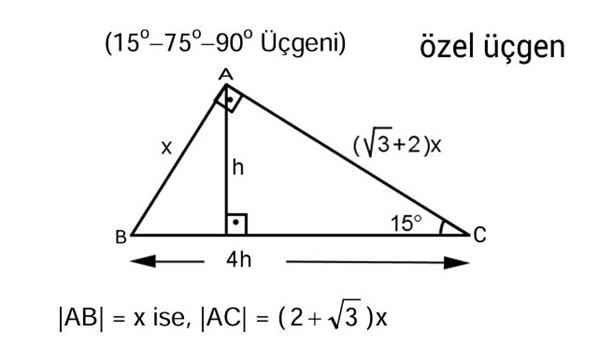
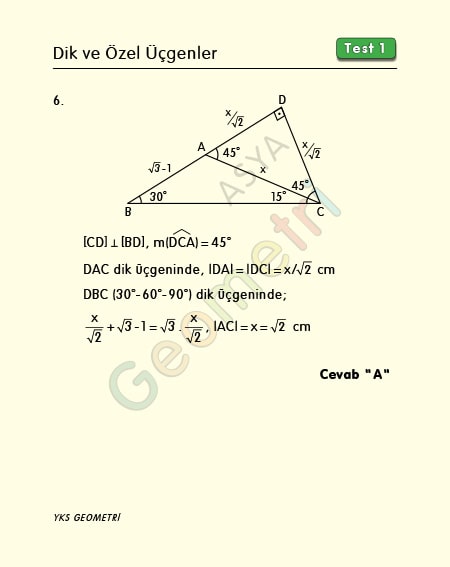
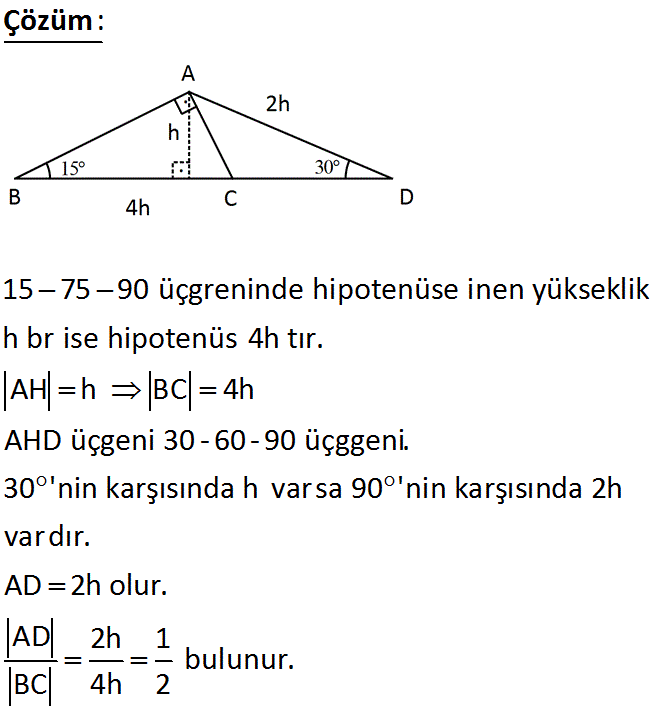
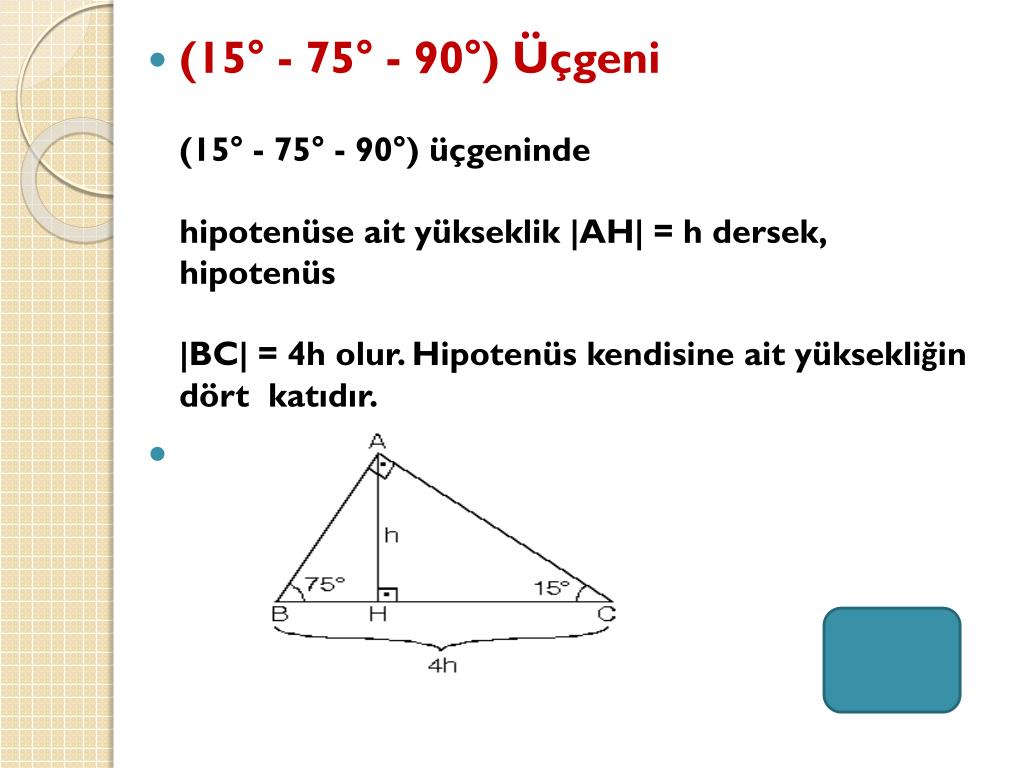
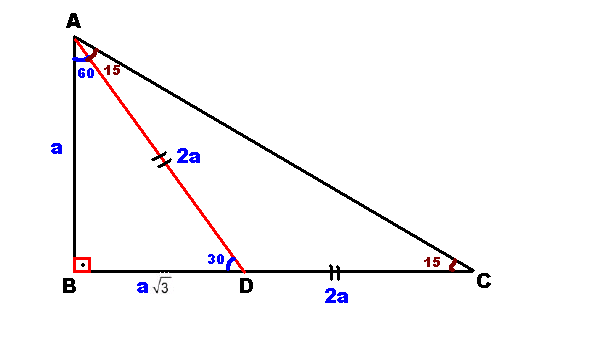
15 75 90 Üçgeni Geometri dersi için önemli özel üçgenlerden olan 15 75 90 üçgeni üçgenin sabit oranından gelmektedir Dik üçgen olan bu üçgende, diğer üçgenlerde olduğu gibi 15 75 90 üçgenin de kenarları arasında sabit oran bulunmaktadır (30° – 60° – 90°) Üçgeni ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABH ve ACH (30° 60° 90°) üçgenleri elde edilir AB = AC = a BH = HC = pisagordan (30° 60° 90°) dik üçgeninde; 30 60 90 üçgeni, bir eş kenar üçgenin iki eşit parçaya bölünmesi ile ortaya çıkmaktadır 30 60 90 derecenin gördüğü kenarların ise belirli kuralları vardır
30 60 90 üçgeni kenarlarıのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「30 60 90 üçgeni kenarları」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「30 60 90 üçgeni kenarları」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「30 60 90 üçgeni kenarları」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「30 60 90 üçgeni kenarları」の画像ギャラリー、詳細は各画像をクリックしてください。
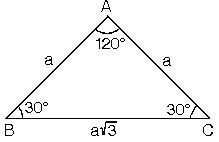 | 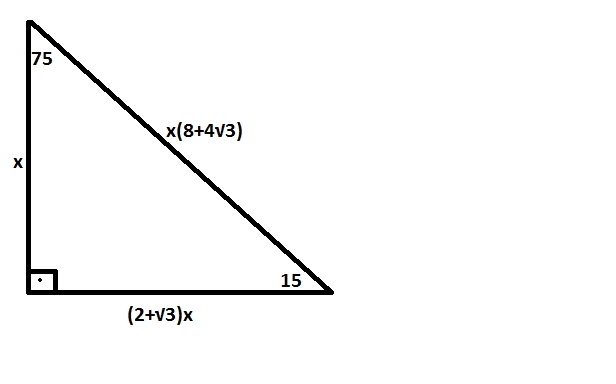 |  |
 |  | |
 |  | |
「30 60 90 üçgeni kenarları」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「30 60 90 üçgeni kenarları」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | 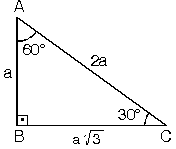 |  |
「30 60 90 üçgeni kenarları」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「30 60 90 üçgeni kenarları」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「30 60 90 üçgeni kenarları」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「30 60 90 üçgeni kenarları」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「30 60 90 üçgeni kenarları」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
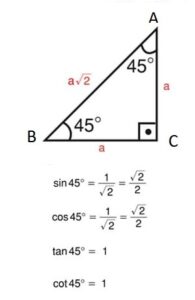
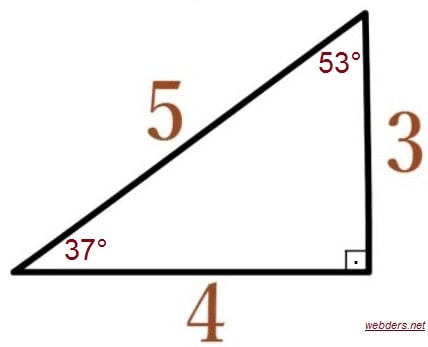
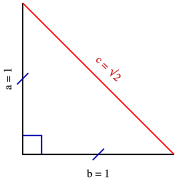
Üçgenin dik kenarları birbirine eşit ve hipotenüsü dik kenarların katıdır Oran aşağıdaki gibidir İspatı ise çok basittir Bir dik kenara 1 cm denilirse, ikizkenarlıktan dolayı diğer dik kenar da 1 cm olmak zorundadır Pisagor Teoremi'nden de hipotenüs çıkar 2 Üçgeni üçgeni ve ispatıİç açıları 30°, 60° ve 90° olan üçgenlere 30 60 90 üçgeni denir Bu üçgenlerin kenarları arasında daima belli bir oran vardır 30 60 90 üçgeninde, 30° nin karşısındaki kenarın uzunluğu hipotenüs uzunluğunun yarısına, 60° nin karşısındaki kenarın uzunluğu hipotenüs uzunluğunun yarısının √3
Incoming Term: 30 60 90 üçgeni kenarları,
コメント
コメントを投稿